[零基础学Python]集合的关系
admin
2023-07-31 01:48:40
0次

冻结的集合

前面一节讲述了集合的基本概念，注意，那里所涉及到的集合都是可原处修改的集合。还有一种集合，不能在原处修改。这种集合的创建方法是：

>>> f_set = frozenset(\"qiwsir\")     #看这个名字就知道了frozen，冻结的set
>>> f_set
frozenset([\'q\', \'i\', \'s\', \'r\', \'w\'])
>>> f_set.add(\"python\")             #报错
Traceback (most recent call last):
  File \"\", line 1, in 
AttributeError: \'frozenset\' object has no attribute \'add\'

>>> a_set = set(\"github\")           #对比看一看，这是一个可以原处修改的set
>>> a_set
set([\'b\', \'g\', \'i\', \'h\', \'u\', \'t\'])
>>> a_set.add(\"python\")
>>> a_set
set([\'b\', \'g\', \'i\', \'h\', \'python\', \'u\', \'t\'])

集合运算

先复习一下中学数学（准确说是高中数学中的一点知识）中关于集合的一点知识，主要是唤起那痛苦而青涩美丽的回忆吧，至少对我是。

元素与集合的关系

元素是否属于某个集合。

>>> aset
set([\'h\', \'o\', \'n\', \'p\', \'t\', \'y\'])
>>> \"a\" in aset
False
>>> \"h\" in aset
True

集合与集合的纠结

假设两个集合A、B

  • A是否等于B，即两个集合的元素完全一样

在交互模式下实验

>>> a           
set([\'q\', \'i\', \'s\', \'r\', \'w\'])
>>> b
set([\'a\', \'q\', \'i\', \'l\', \'o\'])
>>> a == b
False
>>> a != b
True
  • A是否是B的子集，或者反过来，B是否是A的超集。即A的元素也都是B的元素，但是B的元素比A的元素数量多。

实验一下

>>> a
set([\'q\', \'i\', \'s\', \'r\', \'w\'])
>>> c
set([\'q\', \'i\'])
>>> c>> c.issubset(a)   #或者用这种方法，判断c是否是a的子集
True
>>> a.issuperset(c) #判断a是否是c的超集
True

>>> b
set([\'a\', \'q\', \'i\', \'l\', \'o\'])
>>> a>> a.issubset(b)   #或者这样做
False
  • A、B的并集，即A、B所有元素，如下图所示

>>> a
set([\'q\', \'i\', \'s\', \'r\', \'w\'])
>>> b
set([\'a\', \'q\', \'i\', \'l\', \'o\'])
>>> a | b                       #可以有两种方式，结果一样
set([\'a\', \'i\', \'l\', \'o\', \'q\', \'s\', \'r\', \'w\'])
>>> a.union(b)
set([\'a\', \'i\', \'l\', \'o\', \'q\', \'s\', \'r\', \'w\'])
  • A、B的交集，即A、B所公有的元素，如下图所示

>>> a
set([\'q\', \'i\', \'s\', \'r\', \'w\'])
>>> b
set([\'a\', \'q\', \'i\', \'l\', \'o\'])
>>> a & b       #两种方式，等价
set([\'q\', \'i\'])
>>> a.intersection(b)
set([\'q\', \'i\'])

我在实验的时候，顺手敲了下面的代码，出现的结果如下，看官能解释一下吗？（思考题）

>>> a and b
set([\'a\', \'q\', \'i\', \'l\', \'o\'])
  • A相对B的差（补），即A相对B不同的部分元素，如下图所示

>>> a
set([\'q\', \'i\', \'s\', \'r\', \'w\'])
>>> b
set([\'a\', \'q\', \'i\', \'l\', \'o\'])
>>> a - b
set([\'s\', \'r\', \'w\'])
>>> a.difference(b)
set([\'s\', \'r\', \'w\'])

-A、B的对称差集，如下图所示

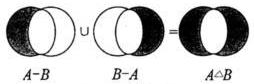
>>> a
set([\'q\', \'i\', \'s\', \'r\', \'w\'])
>>> b
set([\'a\', \'q\', \'i\', \'l\', \'o\'])
>>> a.symmetric_difference(b)
set([\'a\', \'l\', \'o\', \'s\', \'r\', \'w\'])

以上是集合的基本运算。在编程中，如果用到，可以用前面说的方法查找。不用死记硬背。

python

上一篇：【No.001】urllib2.URLError: <urlopen error unknown url type: https> 解决办法

下一篇：[零基础学Python]一二三,集合了

相关内容

热门资讯

Mobi、epub格式电子书如... 在wps里全局设置里有一个文件关联，打开，勾选电子书文件选项就可以了。
定时清理删除C:\Progra... C:\Program Files (x86)下面很多scoped_dir开头的文件夹 写个批处理 定...
scoped_dir32_70... 一台虚拟机C盘总是莫名奇妙的空间用完，导致很多软件没法再运行。经过仔细检查发现是C:\Program...
500 行 Python 代码... 语法分析器描述了一个句子的语法结构，用来帮助其他的应用进行推理。自然语言引入了很多意外的歧义，以我们...
小程序支付时提示：appid和... [Q]小程序支付时提示：appid和mch_id不匹配 [A]小程序和微信支付没有进行关联，访问“小...
pycparser 是一个用... `pycparser` 是一个用 Python 编写的 C 语言解析器。它可以用来解析 C 代码并构...
微信小程序使用slider实现... 众所周知哈，微信小程序里面的音频播放是没有进度条的，但最近有个项目呢，客户要求音频要有进度条控制，所...
65536是2的几次方 计算2... 65536是2的16次方：65536=2⁶ 65536是256的2次方：65536=256 6553...
Apache Doris 2.... 亲爱的社区小伙伴们，我们很高兴地向大家宣布，Apache Doris 2.0.0 版本已于...
项目管理和工程管理的区别 项目管理 项目管理，顾名思义就是专注于开发和完成项目的管理，以实现目标并满足成功标准和项目要求。 工...